Asymmetric Key Encryption
공개 키와 비공개 키 기반의 기술. 평문을 encrypt와 decrypt하기 위해 2개의 다른 키를 사용한다. 대칭 키 암호화 보다 느리다. 대표적인 알고리즘으로는 RSA, 디피-헬만, 타원곡선암호 등이 있다.
개념
A와 B 키가 있다고할 때, A로 암호화한 내용은 오직 B로만 복호화할 수 있고 B로 암호화한 내용은 A로만 복호화할 수 있다는 것이 기본 개념이다.
때문에 하나의 키를 공개하여도 나머지 키만 보호된다면 무관하므로 서로가 상대의 공개 키를 공유하여 이를 해석하는 데에 사용하게되어 배송 문제가 근본적으로 발생하지 않는다.
다만 이러한 비대칭 키는 암복호화가 대칭 키 알고리즘보다 현저히 느려 소규모의 데이터, 또는 대칭 키를 공유하는 데에 활용할 수 있다.
RSA
소인수분해의 어려움에 기반한 암호화 방법.
공개키는 $n$, $e$, 개인키는 $n$, $d$로 이루어져 있다.
키 생성
- 임의의 소수 $p$, $q$를 정하고 $n = p * q$를 하여 $n$의 값을 지정한다.
- $(p - 1) * (q - 1)$ 과 각각 서로소인 e를 고른다.
- $e * d$를 $(p - 1) * (q - 1)$로 모듈러 연산을 수행했을 때 1이 되는 값을 $d$로 정한다.
암복호화
Message를 M, Crypto를 C로 한다.
- 암호화: $C = M^e mod$ n
- 복호화: $M = C ^ d mod$ n
$p = 3, q =5$로 지정하고 M = 5를 암복호화
- $n = 3 * 5 = 15$
- $1 < e < (p - 1) * (q - 1)$ → 1 < e < 8 → e = 5
- gcd(5 * d, 8)인 값 d, d = 3
- $C = 5 ^ 5 mod$ 15 = 3125 mod 15 = 5
- M = 5 ^ 3 mod 15 = 5
입력값이 한정적이라 Crypto가 동일하게 나왔지만 진행된 것을 확인할 수 있다.
공격 방법 및 걸리는 시간
- 소인수분해
- 소인수분해에 기반한 기술이므로 수학적으로 계산해낸다면 암호를 무력화할 수 있다. 다만 키 길이를 길게할 수록 현실적으로 불가능한 수준의 계산 능력을 필요로 하게된다.
- 개인키 유출
- p, q, ϕ(n), d 중 단 하나라도 노출된다면 나머지 키들을 모두 획득할 수 있다.
- 방법은 확장된 유클리드 호제법을 사용하면 간단하게 구할 수 있다.
- 낮은 지수 공격
- 공개 키인 e의 값으로 매우 작은 수를 사용하고 n의 값이 클 때 e 거듭제곱근을 구해서 평문으로 복호화할 수 있다.
- Weiner’s attack
- 기본적으로 e 값이 큰 경우 d 값이 작을 확률이 더 높고, 이를 이용해 공격할 수 있다.
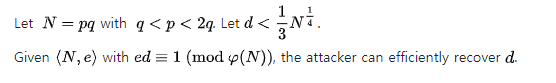
ECC(Elliptic Curve Cryptosystem)
디지털 서명, 비밀키의 안전한 분배, 보안을 요하는 정보의 안전한 전송에 이용된다.
다른 비대칭 암호화 방식에 비해 적은 길이를 가지는 키와 고속의 암호 연산 등의 특징으로 인해 무선 통신, 서명, 인증 등 빠른 속도와 제한된 대역폭 등이 요구하는 무선 통신 분야에 유용한 암호 알고리즘이다.
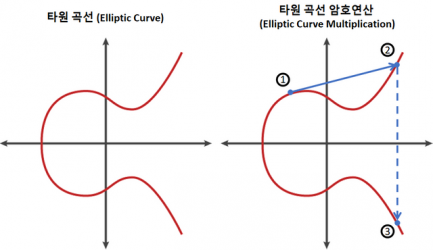
원리
타원 곡선군의 이산 대수 문제에 기반을 둔다.
- 이산 대수 문제(이산 로그 문제:;logrithm):
- $a^x=b$
- 위 식에서 실수 a, b가 주어졌을 때 식을 만족하는 최소의 자연수 K를 찾는 문제이다.
- $x = log(a)b$
- 일반적인 실수 체계에서는 위 log 식을 따르기에 이산 로그 문제라고 부르며 산술적으로 해를 구하기 위한 일반적인 실수 체계와 달리, 군에서는 대소 비교가 원활하지 않기에 어려움이 있다.
- → $log(b) x < log(b) y$를 비교하는 데에 어려움
- 암호학에서는 해당 군을 큰 소수 p에 대해 p로 나눈 나머지들로 사용한다.
- Zp*에서 p는 7이고 $3^5$를 구하는 경우 $243 / 7 = ? ... 5$이므로 $3 ^ 5=5$이다.
- → $log(b) x < log(b) y$를 비교하는 데에 어려움
타원 곡선 암호에서는 3가지의 구성요소가 존재한다.
- 개인키(k): 타원곡선 상에 임의의 점 p를 더하여 새로운 점을 계산하는 함수
- 공개키(kP): P를 k번 더해서 생성되는 새로운 점에 해당되는 값
- 타원 함수: $y^2=x^3+ax+b$
단계
- $P + Q + R = 0$이 되는 점 $P, Q, R$을 선택한다.
- 시작점은 $P$와 $Q$가 중근을 갖는 점을 선택한다. ($P=Q$)
- $P + Q + R = 0, P + P + R = 0, 2P + R = 0, R = -2p$ 따라서 R에 x축에 대칭인 점은 $2P$가 된다.
- 이후 점 $2P$를 점 $P$와 연결하면 $Q = 2P$, $P + 2P = R$ 연산을 재수행한다. 따라서 $R = -3P$이고 X축에 대칭인 점은 3P가 된다.
위 연산은 계속해서 수행할 수 있으며, 특정 시점에서 종료 시 $R=nP$가 된다. 이때 n은 개인키가 되고, nP는 공개키가 된다.
공개키(nP)로 encrypt된 암호문은 개인 키 K를 사용하면 복호화할 수 있고, 반대로 사용 시 디지털 서명이 된다.
- 타원 곡선과 임의의 선이 만나는 교점을 구하여 암호화 키로 이용한다.
- 서로 다른 타원곡선을 선택하여 사용할 수 있어 추가 보안을 위해 주기적으로 타원곡선을 바꿀 수 있다.
공격 방법 및 걸리는 시간
- 프라이빗 키가 공개되지 않는 이상, 난수의 길이가 충분히 길다면 현실적으로 암호를 해독하는 것이 불가능하다.
Symmetric Key Encryption vs Asymmetric Key Encryption
| 대칭 키 | 비대칭 키 |
|---|---|
| encryption와 decryption에 오직 하나의 키만 필요 | encryption와 decryption에 public key와 private key가 필요 |
| 암호문이 원본 데이터와 같거나 더 작음 | 암호문이 원본 데이터와 같거나 더 큼 |
| 암호화 과정이 매우 빠름 | 암호화 과정이 매우 느림 |
| 대량의 데이터가 이동할 시에 사용됨 | 작은 양의 데이터가 이동할 적에 사용됨 |
| 128 or 256 btis의 키 길이를 가짐 | 2048 또는 그 이상의 길이를 가짐 |
'암호학' 카테고리의 다른 글
| Digital Signature (0) | 2023.10.14 |
|---|---|
| Message Authentication && Hashing (0) | 2023.10.14 |
| Symmetric Key Encipherment (0) | 2023.10.04 |
| AESAdvanced-Encryption-Standard-algorithm (0) | 2023.06.10 |